Stocking the Bar

Experimenting with cocktails and the myriads of flavors and presentations can be a delightful culinary avocation. However, stocking a bar is expensive. Different mixing alcohols typically range from 10-50 USD and you also need a swarm of other syrups, garnishes, and toppers. Even with a reasonable selection of bottles one can still find themselves with a lackluster number of cocktails that they can make. After going through this morose experience myself I began to wonder what an ideal set of cocktail ingredients would be. As it turns out this problem can be solved (sort of) with some old fashioned computer science.

Finding the Right Ingredients

So how do we go about finding an optimally stocked bar? First, we need to define what optimal is. But before I lay out the objective, let us define a couple of terms. Let \(R\) and \(I\) be the set of all recipes and ingredients, respectively. We will say a set of ingredients \(A \subseteq I\) satisfies a recipe \(r \in R\) if \(r\) can be made using the ingredients in \(A\).

The most interesting problem (at least to me) is given a positive integer \(k\) can we find the set of ingredients of size at most \(k\) that satisfy the largest number of recipes. I.e. if we are only allowed \(k\) ingredients, how do we select these ingredients such that we can make the most recipes with them. This can be notated as:

Here \(\mathbb{1}_{\{A\ \textrm{satisfies}\ r\}}\) is an indicator function that is \(1\) when the ingredients \(A\) satisfies the recipes \(r\) and \(0\) otherwise.

A Brute-Force Solution

A more algorithmic friendly way to write our problem is by considering the related problem of what recipes do not need a list of ingredients. In this sense let \(R_i \subseteq R\) be the set of recipes that do not use ingredient \(i\in I\). The intersection of these sets, for instance \(R_i \cap R_j \cap R_k\), represents the set of all recipes that do not use ingredients \(i, j,\) and \(k\). Now finding the largest intersection of at most \(\lvert I \rvert - k\) of these subsets will give the largest set of recipes that can be made with \(k\) ingredients. The brute-force algorithm for this can be expressed rather simply.

# create list of subsets R_i for each ingredient i; R_i is all recipes that can be made without i 
subsets = set(frozenset(r for r in recipes if not r.uses_ingredient(i)) for i in all_ingredients)

max_subsets = max(combinations(subsets, len(subsets)-k), key=lambda s: len(frozenset.intersection(*s)))

This algorithm is equivalent to the minimum \(k\)-union problem and has been proven to be NP-Hard [1]. In the worst case it will iterate over \(\binom{\lvert I\rvert}{\lvert I\rvert-k}\) combinations of sets and compute their intersection size. While the number of recipes \(\lvert R\rvert\) impacts the duration to compute the set intersections, this complexity is largely dominated by the \(\lvert I\rvert !\) factorial term. Thus, it is necessary to keep this term small so that the brute-force algorithm can finish in a reasonable amount of time. Fortunately, the number of unique ingredients likely lies between 20 and 100 for a reasonable list of recipes making it easy to keep small. We also benefit from the fact that this algorithm is likely being run with very small values of \(k\) as that is of most interest.

We can further reduce the number of ingredients, \(\lvert I \rvert\), with a couple of data set augmentations. First, we can remove unnecessary ingredients from recipes. This includes any items we are likely to already possess, such as ice, water, salt, sugar, etc. We can also remove garnishes from the recipes if we just care about the main drink. Additionally, we can make substitutes where applicable so as to reduce the total number of unique ingredients. For example, we may replace instances of Rye Whiskey or Bourbon with just Whiskey. These three optimizations can meaningfully reduce the total search space for the brute-force algorithm.

Other Algorithms

Using the reduced ingredients set from the brute-force algorithm I have also implemented several other algorithms and heuristics for comparison. These are detailed below.

k Most Common Ingredients

Here we compute the number of occurrences of each ingredient across all recipes and take the \(k\) most common. This could potentially yield the optimal solution or the worst case of 0 total recipes. It has the benefit of a good time complexity: counting is \(O(\lvert I\rvert)\) and finding the \(k\) most common is \(O(\lvert I\rvert\log k)\) with a heap queue. For a small fixed \(k\) this is linear in \(\lvert I\rvert\).

Max Recipe Degree

Construct a graph \(\mathcal{G}_R=(V,E)\) where \(V=R\) and \((r_i, r_j)\in E\) iff \(r_i\) and \(r_j\) share an ingredient. Also constructed a weighted version of \(\mathcal{G}_R\) where \(w_{r_i,r_j}\) is equal to the number of shared ingredients between \(r_i\) and \(r_j\).

Now select the max degree vertex \(v^* = \max_{v\in V}\deg v\) and remove it from the graph. Update a set with the ingredients of \(v^*\). Continue this process until the set being built has size \(\ge k\) or the graph is empty. Select the built set as the final list of ingredients.

The time complexity is dominated by the graph construction which is roughly \(O(\lvert R\rvert^2)\).

Max Ingredient Degree

Similar to above construct a graph \(\mathcal{G}_I=(V,E)\) where \(V=I\) and \((i_m, i_n)\in E\) iff \(i_m\) and \(i_n\) are in a recipe together. The weight of the edge \(w_{i_m,i_n}\) is the total number of recipes that have both \(i_m\) and \(i_n\).

Select and remove the highest degree vertex \(v^*=\max_{v\in V}\deg v\). Do this \(k\) times or until the graph is empty. The \(k\) removed vertices are the final selected set of ingredients.

Greedy

Instead of fixing the ingredients this algorithm fixes the number of recipes to \(k\) and tries to find the smallest number of ingredients that satisfy at least \(k\) recipes.

Let \(A=\{\}\) be an empty set of recipes. Pick a recipe \(r^*\in R\) thats ingredients minimize the union of \(A\) and the ingredients of \(r^*\), i.e. \(r^* = \min_{r\in R}\lvert A \cup r\rvert\). Remove \(r^*\) from \(R\) and update \(A\) such that \(A=A\cup r^*\). Repeat this process \(k\) times.

This guarantees that the ingredients in \(A\) satisfy at least \(k\) recipes. At each step we take the locally optimal solution making this a greedy algorithm. We end up computing \(O(k\lvert R\rvert)\) unions making this a fairly fast heuristic algorithm.

Random Sampling

This is just to serve as a benchmark. We take \(M\) random subsets of size \(k\) from \(I\). The one that satisfies the most recipes is selected.

When testing I use an alternate method where I continue sampling until a certain duration has passed (1 second). Once that duration has passed the best subset found during sampling is selected.

Results

I implemented all of the above in Python to compare their results and runtimes. This code can be found here. For input I used a hand-compiled set of 25 cocktail recipes found from various internet sites. Before running the algorithms the garnishes are filtered out and substitutions for common ingredients are made as described in the brute-force algorithm.

It should be noted that the brute-force exhaustive algorithm was only run up to \(k=10\) due to time limits. Additionally, due to the use of sets and Python 3’s non-deterministic hash functions the final list of ingredients found by each algorithm is non-deterministic (however, its size is).

The first figure, depicted below, shows the number of recipes satisfied (\(y\)-axis) by the returned list of ingredients (\(x\)-axis). Each line represents a different algorithm.

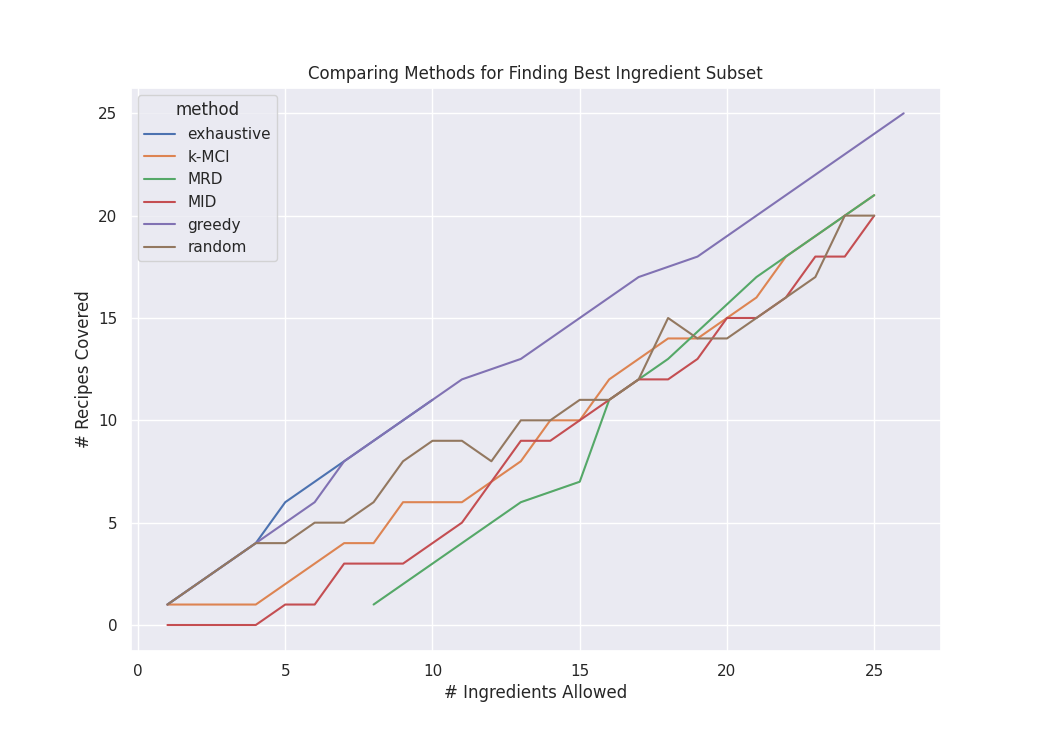
We see that greedy performs very near the brute-force solution (note: exhaustive cuts off after \(k=10\) due to time limits). The rest all perform similarly with result sizes about 3-4 lower than the optimal.

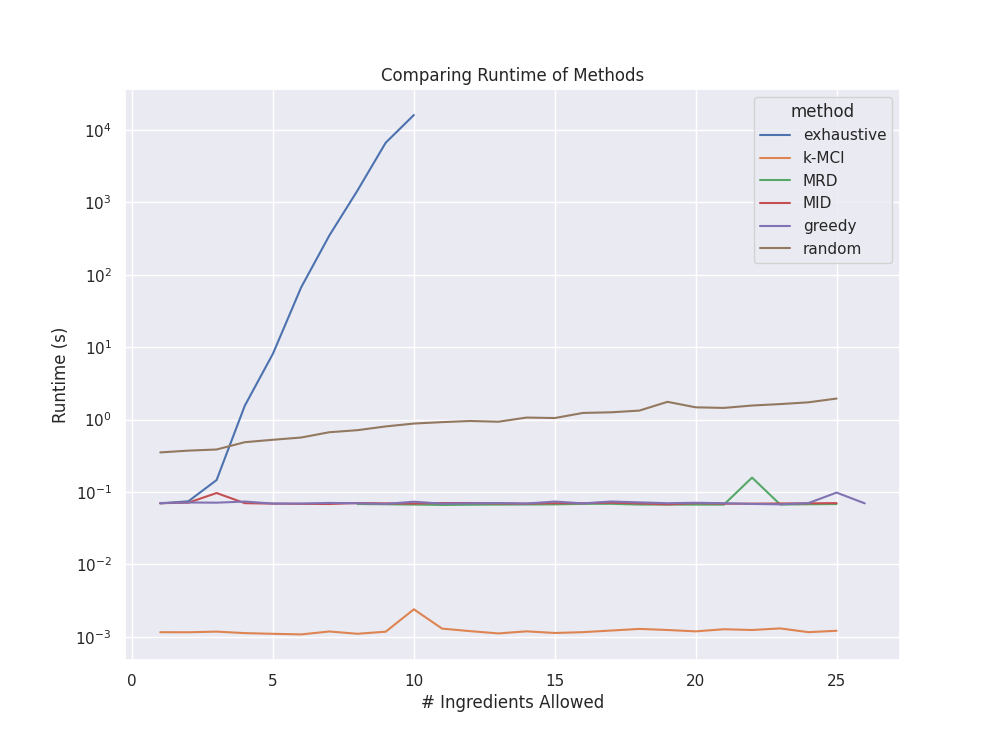
Furthermore, the next figure highlights the runtime of each algorithm. Note the \(y\)-axis is log scale 10. As expected we see an exponential blow up in runtime for the brute-force solution. This algorithm, while exact, is infeasible for realistically sized data sets. Combined with the above results we can conclude that the greedy algorithm is the best in terms of result to performance trade-off.

The Best Ingredients

The numbers are indeed interesting, but what is the best subset of ingredients? This what we initially set out for after all. Running the brute-force algorithm with \(k=10\) on my small recipe data set we get the following list of ingredients.

Cola, Cream, Lemon Juice, Vermouth, Gin, Campari, Whiskey, Beer, Tonic, Bitters

These, plus common household ingredients and garnishes, can be used to make the following 11 recipes.

Negroni, Hot Toddy, Jack and Coke, Boulevardier, Dry Martini, Gin Tonic, 
Boilermaker, Manhattan, Old Fashioned, Irish Coffee, Whiskey Neat

Note that these results are severely impacted by the data set used. For example I could artificially inflate the result by adding recipes to my list that are just combinations of these 10 ingredients. Thus, the scale of these numbers, 10 ingredients and 11 recipes, is not as interesting, but rather their optimality for this particular \(R\) and \(I\). In this case, since we used the brute-force algorithm, we can conclude that this is the optimal solution for our particular list of recipes.

For \(k=5\) the brute force algorithm gives the following.

Ingredients: Gin, Vermouth, Whiskey, Campari, Bitters
Recipes: Old Fashioned, Dry Martini, Boulevardier, Negroni, Whiskey Neat, Manhattan

For larger \(\lvert I\rvert\) and/or \(k\) we will need to switch to the greedy heuristic algorithm. However, we have previously demonstrated that this algorithm is a good candidate for finding good ingredient sets.