Recursive Doubling

Consider a problem of the form

where \(x_1=b_1\) and \(a_i,b_i,x_i \in \mathbb{R}\). When \(a\) and \(b\) are known computing \(x\) appears to be an intrinsically serial problem. To compute \(x_i\) you must know \(x_{i-1}\). The code would look something like below.

x[0] = b[0];
for (size_t i = 1; i < n; i++) {
  x[i] = a[i] * x[i-1] + b[i];
}

However, we can approach in a parallel manner when we consider some observations.

Observation #1: \(x_i\) can be rewritten in terms of \(x_{i-2}\).

Just using Observation #1 we can already see room for parallelization. The odd and even indices of \(x\) can be computed in parallel. Using OpenMP here is the code using Observation #1 alone.

x[0] = b[0];
x[1] = a[1] * x[0] + b[1];
#pragma omp parallel {
  int thread_idx = omp_get_thread_num();
  if (thread_idx == 0) {
    for (size_t i = 3; i < n; i += 2) {
      x[i] = a[i] * a[i-1] * x[i-2] + a[i] * b[i-1] + b[i];
    }
  } else if (thread_idx == 1) {
    for (size_t i = 2; i < n; i += 2) {
      x[i] = a[i] * a[i-1] * x[i-2] + a[i] * b[i-1] + b[i];
    }
  }
}

In fact, we can use #1 to speedup without parallel computing. Consider the below loop:

x[0] = b[0];
for (size_t i = 1; i < n; i += 2) {
  // (1)
  x[i] = a[i] * a[i-1] * x[i-2] + a[i] * b[i-1] + b[i];
  // (2)
  x[i+1] = a[i+1] * a[i] * x[i-1] + a[i+1] * b[i] + b[i+1];
}

In the for loop we see that (1) sets \(x_i\) using \(x_{i-2}\) and (2) sets \(x_{i+1}\) using \(x_{i-1}\). Therefore, there are no overlap in dependencies and the code is valid. But we’re still serial, so why is this loop faster than the other one? Cache efficiency. \(x\) is stored contiguously in memory. When we load two consecutive values of \(x\) at once (\(x_{i-2}\) and \(x_{i-1}\)) we can do it with roughly the cost of one load, because these two values will lie within the same cache line. We are also effectively loop unrolling as we have reduced the number of loop iterations by a factor of 2.

We can see an immediate effect from these two methodologies in the plot below:

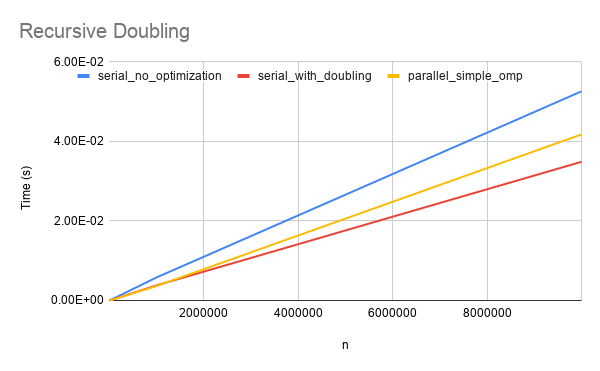
Now we’ve seen that we can compute the odd and even indices of \(x\) in parallel. Can we re-index these two subsets and recursively split our lists?

Observation #2: To compute any \(x_i\) from a given \(x_{i-N}\) we can use

This is a powerful observation as we can now calculate any \(x_i\) with any \(x_j\) where \(j<i\).

W.I.P…